|
Έχω μπροστά μου εδώ και δέκα μέρες το νέο πρόγραμμα σπουδών
θέλω να γράψω την γνώμη μου αλλά διστάζω. Ο πρώτος λόγος: δεν ξέρω απο που να
αρχίσω και που να καταλήξω. Ο δεύτερος: η ελπίδα ότι , με τις μέρες, θα
προκύψει ένα ήπιο κείμενο όπως λογικά θα άρμοζε σε ένα θέμα της Τέχνης μας και
της Επιστήμης μας.
Η παραγωγή των τελευταίων προγραμμάτων σπουδών έγινε σε δύο επίπεδα
α) από μία Επιτροπή
Συντονιστών Αξιολογητών και Αξιολογητών που επελέγη πρώτη.
β) από μία επιτροπή Σύνταξης
Προγραμμάτων που αντλήθηκε από ένα μητρώο
εμπειρογνωμόνων που επελέγη στη συνέχεια.
Δεν είμαι σε θέση να γνωρίζω ακριβώς ποιοί τελικά μετείχαν στην σύνταξη των
προγραμμάτων. Αυτό που γνωρίζω με βεβαιότητα είναι ότι ο υπ΄αριθ 12 στην λίστα
των μαθηματικών τελικά δεν συμμετείχε. Η βεβαιότητα αντλείται από το γεγονός
ότι πρόκειται για μένα: με λύπη μου παραιτήθηκα πριν καν ολοκληρωθεί η πρώτη
συνεδρία. Γνωρίζω με τον ένα ή τον άλλο τρόπο τους περισσότερους από τους
συμμετέχοντες. Κάποιοι είναι φίλοι-συνεργάτες. Παρά το γεγονός ότι πιστεύω ότι
οι ευθύνες στον βίο μας είναι πρωτίστως προσωπικές εν τούτοις δεν είναι στις
προθέσεις μου να αναφερθώ σε πρόσωπα. Θα αναφερθώ σε πράξεις και αναγκαστικά σε
ιδέες που, κατά την γνώμη μου, τις υποβαστάζουν. Στα επόμενα ακολουθούν μερικές
κατά την γνώμη μου βασικές επισημάνσεις. Το θέμα είναι τεράστιο και αναγκαστικά
θα επανέλθουμε.
00) Η επιτροπή
αξιολόγησης που επελέγη πρώτη προχώρησε σε ένα πολύ σφιχτό επιμερισμό της ύλης
ανά μάθημα/τάξη/κατεύθυνση. Ουσιαστικά έλαβε βασικές αποφάσεις οι οποίες
γνωστοποιήθηκαν στα μέλη των επιτροπών β) λίγο πριν την πρώτη συνάντηση τους.
Το σχετικό κείμενο μπορεί να βρεθεί εδώ.
Το κείμενο αυτό δημιούργησε ένα είδος τετελεσμένου που εν πολλοίς δέσμευε τις
επιτροπές σύνταξης των προγραμμάτων. Αν δει κανείς προσεκτικά οι αποκλίσεις του
τλικού σχεδίου από το αρχικό είναι μικρές. Όπου υπάρχουν είναι προς τα κάτω
και για αυτό υπάρχει κάποια εξήγηση..
01) Ένα αναλυτικό
πρόγραμμα ή πρόγραμμα σπουδών πείτε το όπως θέλετε αποτελεί πρωτίστως μία
πολιτισμική επιλογή. Ως τέτοια προσδιορίζει την θέση της Εκπαίδευσης και
εξ΄ωθήσεως της Παιδείας σε σχέση με την πολιτισμική παράδοση. Αλλά και το
μέλλον. Κατά μεταφορά ισχύει αυτό που μας παρέδωσε ο Εγγονόπουλος και διέδωσε ο
Σαββόπουλος: "εδώ δεν είναι παίξε γέλασε: εδώ είναι Μπαλκάνια".
Κοντολογής ουδείς (της επιτροπής αξιολόγησης συμπεριλαμβανομένης) δικαιούται να
παίζει με αυτό που αποτελεί εμπεδωμένη μαθηματική παράδοση.
Παράδειγμα 1. Η επινόηση των Μιγαδικών Αριθμών αποτελεί μείζον
πολιτισμικό επίτευγμα. Πέρα από τις εφαρμογές τους μας δίνουν την δυνατότητα να
καταλάβουμε πολλές όψεις των Μαθηματικών. Οι συμμαθητές μου φεύγοντας από το
Κλασικό Εξατάξιο Γυμνάσιο (εν έτει 1971 για πληροφόρηση σας) είχαν ακούσει μιγαδικούς
αριθμούς από τα 16 τους. Οι συντάκτες των προγραμμάτων πρέπει να διέθεταν
περισσή αναίδεια (τα λεξικά μου με πληροφορούν ότι πρόκειται για έλλειψη αιδούς
και αιδώς=συναίσθημα ντροπής, συστολή, σεβασμός, κοσμιότητα προς τους άλλους
αλλά και αυτοσεβασμός, αίσθημα τιμής, φιλοτιμία κ.α) για να αφαιρέσουν από τις
σπουδές των Ελληνοπαίδων για τα επόμενα χρόνια όσα μας έπεισαν να διδάξουμε οι
σοφοί παππούδες μας.
Παράδειγμα 2. Η Τριγωνομετρία συρρικνώνεται ουσιαστικά στην διδασκαλία
των τριγωνομετρικών συναρτήσεων. Είναι όμως γνωστό ότι η αξία των
τριγωνομετρικών συναρτήσεων, από μόνων τους, έγινε κατανοητή τον 19ο αιώνα με
τις σειρές Fourier. Πιο πριν αλλά και μετά οι άνθρωποι χρησιμοποιούσαν τους
τριγωνομετρικούς αριθμούς για να επιλύουν τρίγωνα και τετράπλευρα. Και ας
βρεθεί κάποιος διαπιστευμένος στην φρενίτιδα της αναζήτησης προβλημάτων-μαϊμού
να προτείνει ένα πρόβλημα που να ανταγωνίζεται σε ενδιαφέρον, ισχύ και
αισιοδοξία το πρόβλημα του υπολογισμού της απόστασης δύο απρόσιτων σημείων.
Τριγωνομετρία χωρίς επίλυση τριγώνων δεν λέει. Ας σημειωθεί ότι εκτός από την
απάλειψη της διδασκαλίας βασικών τύπων οι νόμοι ημιτόνων συνημιτόνων
παρουσιάζονται μετέωροι μακριά από την φυσική τους κοίτη που είναι η Γεωμετρία
(βλ. σ 1961, 2008)
Παράδειγμα 3. Η Γεωμετρία, η διδασκαλία της, η απόδοση σε αυτήν της
πρέπουσας αξίας αποτελεί βασική πολιτισμική επιλογή. Και η απόδοση αξίας σε
όσους μαθητές μοχθούν σε αυτήν επίσης. Στα χρόνια μου η γνώση της Γεωμετρίας
διαδραμάτιζε σημαντικό ρόλο στην μετέπειτα πορεία ενός μαθητή διότι εξετάζονταν
στις εξετάσεις για τα Πανεπιστήμια-Πολυτεχνεία. Μετά από μακροχρόνιο εξοβελισμό
της πριν λίγα χρόνια τα πράγματα άρχισαν να αλλάζουν. Η αμέσως προηγούμενη
επιτροπή Προγραμμάτων είχε (το γνωρίζω γιατί είχα την τιμή να μετέχω) δρομολογήσει
την διδασκαλία της Γεωμετρίας στην Γ΄Λυκείου και την εξέταση της στις
πανελλήνιες. Στα προγράμματα που εξετάζουμε η Γεωμετρία (μιλάμε για την
συνθετική Γεωμετρία) έχει στριμωχτεί στην Α΄και Β΄Λυκείου. Η δε Στερεομετρία
(θετική επιλογή η επαναφορά της) στριμώχνεται στο τέλος της ύλης των δύο αυτών
τάξεων. Η Γερμανική παροιμία "Τον τελευταίο τον τρώει ο λύκος"
βρίσκει πλήρη εφαρμογή. Όλο και κάποια εγκύκλιος θα βγει που θα λέει να μην
διδαχθεί!
Παράδειγμα 4. Η Θεωρία Αριθμών. Σε πείσμα των όσων έγραφε ο Hardy στη
"Απολογία" του η Θεωρία Αριθμών ουδόλως άχρηστη είναι. Πέρα από το
ότι είναι ένα μέρος των Μαθηματικών που το τοπίο του γίνεται εύκολα αντιληπτό
είναι γοητευτική και εφαρμόσιμη. Χρειάζεται αρκετή συλλογική
στενοκεφαλιά για να εξοστρακιστεί από το πρόγραμμα σπουδών. Τα σημαντικά
πράγματα είναι και χρήσιμα . Όσους δεν το καταλαβαίνουν οφείλουμε να
τους παρακάμπτουμε όπως, σύμφωνα με τον Στοβαίο, έπραξε ο Ευκλείδης που ζήτησε
από τον δούλο του να δώσει, ως αντάξια προσβολή, το κάτι τις του σε εκείνον που
αναρωτιόταν τι θα κερδίσει (εδώ και τώρα) αν μάθει Μαθηματικα. Τα
σημαντικά πράγματα είναι και χρήσιμα όπως ψέλισε ένας ήρωας της ταινίας
"Η Λίστα του Σίντλερ": "I teach history and literature. Since
when it's not essential?"
02)
Η Άλγεβρα στη γωνία. Στο πρόγραμμα της Άλγεβρας διακρίνεται μία
κυριαρχία των συναρτήσεων. Αυτό προφανώς ως συνέπεια μιας αντίληψης που
χοντρικά λέει "όλα είναι συναρτήσεις". Η αντίληψη αυτή έχει και
συνέχεια: Δίνει την εντύπωση ότι πλείστα μαθηματικά ζητήματα μπορούν να
μελετηθούν με γραφικές παραστάσεις συναρτήσεων με λογισμικό και τις
υπερτιμημένες ΤΠΕ. Το ότι η συνάρτηση είναι σημαντική έννοια είναι σωστό.
Ωστόσο η έννοια της συνάρτησης δεν είναι αρκετή για να μας δώσει όλη την
εικόνα. Και η εμμονή να διαθλώνται όλα μέσω των συναρτήσεων δημιουργεί
εσφαλμένες αντιλήψεις.
Παράδειγμα 1. Δεν είναι η συνάρτηση 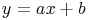 που περιγράφει ευθείες
αλλά η σχέση των x,y: που περιγράφει ευθείες
αλλά η σχέση των x,y: 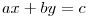 με με 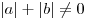 .
Βέβαια όταν φθάνουμε στις κωνικές τομές όπου δεν έχουμε συναρτήσεις οι
συντάκτες του προγράμματος (σελίδα 2157) το αναγνωρίζουν. .
Βέβαια όταν φθάνουμε στις κωνικές τομές όπου δεν έχουμε συναρτήσεις οι
συντάκτες του προγράμματος (σελίδα 2157) το αναγνωρίζουν.
Παράδειγμα 2. Οι πράξεις είναι όντως συναρτήσεις. Η διάταξη μπορεί να
περιγραφεί με την βοήθεια συναρτήσεων. Ωστόσο αυτό είναι ένα γεγονός χωρίς
μετατρέψιμη αξία για τους μαθητές. Η τάση να θεωρούνται όλα συναρτήσεις μερικές
φορές οδηγεί και σε ακραίες καταστάσεις. Τι θα απαντούσαν οι συντάκτες του
προγράμματος στην ερώτηση ενός μαθητή πως θα είναι η συνάρτηση θέσης της
κάμπιας στην σελίδα 1964;
Η εμμονή στις συναρτήσεις ωθεί τους μαθητές να βλέπουν τα πάντα ως συνάρτηση.
Όσοι δουλεύουν στα σχολεία θα έχουν διαπιστώσει την κατάχρηση του "θέτω f(x)=...." (Δείτε και την
ανάρτηση Η
κατάρρευση της Άλγεβρας.
Θα ήθελα όμως να σημειώσω ότι η επιλογη της θέασης μέσω συναρτήσεων δεν
ακολουθείται με συνέπεια. Θα ανέμενε κάποιος σε κάθε μελέτη ειδικής περίπτωσης
μιας συνάρτησης να εξετάζεται η αντίστοιχη εξίσωση και ανίσωση
-Με την διδασκαλία της
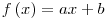 εξετάζεται
η εξίσωση
εξετάζεται
η εξίσωση 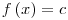 και η
ανίσωση και η
ανίσωση 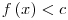 . .
-Με την διδασκαλία της
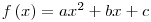 εξετάζεται
η εξίσωση εξετάζεται
η εξίσωση 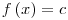 και η
ανίσωση και η
ανίσωση 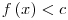 . .
-Με την διδασκαλία της
 εξετάζεται η εξίσωση εξετάζεται η εξίσωση 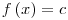 και η
ανίσωση και η
ανίσωση 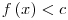 . .
Όπως φαίνεται αυτή παρουσίαση που μεταξύ άλλων βάζει σε τάξη κάποια πράγματα
δεν ακολουθείται.
'Ομως δεν είναι μόνο ο υπερτονισμός των συναρτήσεων προβληματικός. Είναι και ο
παραμερισμός χρήσιμων αλγεβρικών γνώσεων και δεξιοτήτων: ταυτότητες υπό
συνθήκη, απόδειξη ανισοτήτων, ανάδειξη της παραμέτρου, σχέσεις συντελεστών
ριζών στα πολυώνυμα τουλάχιστον β΄βαθμού).
Αυτή η επιλογή των συντακτών έχει ως συνέπεια και τον περιορισμό του ρόλου των
αποδεικτικών διαδικασιών στην Άλγεβρα την απόκρυψη της δομής της και την
εξομοίωση της με ένα πλήθος ασύνδετων κανόνων προς εφαρμογή συν ένα μενού από
επίσης ασύνδετες "δραστηριοτήτες".
03) Η
μεταλλαγμένη Ανάλυση. 'Εγραψα πιο πριν ότι η απόκλιση του αρχικού
σχεδίου προγράμματος με το τελικό έγινε προς τα κάτω. Ένα χτυπητό παράδειγμα
είναι η ανάλυση. Πλήρως απονευρωμένη από τα βασικά, ωραία και χρήσιμα θεωρήματα
της παραδίδεται ως ένα ακρωτηριασμένο ον που ούτε Calculus είναι ούτε
στοιχειώσης Ανάλυση. Το επιχείρημα που πρόλαβα να ακούσω ήταν ότι τα υπαρξιακά
θεωρήματα οδηγούν σε ανευ συγκρατημού άχρηστη ασκησιολογία. Φυσικά αυτό δεν
είναι ακριβές: Όντως παράγονται και διδάσκονται άπειρα σκουπίδια με την
αναζήτηση των "ξ" δια παν ενδεχόμενο θέμα.
Αν "κλειδώσει" με οδηγίες διδασκαλίας η ρήτρα ότι τέτοιου είδους
θέματα δεν εξετάζονται το θέμα τελειώνει. Παραμένουν τα θεωρήματα, οι
ενδιαφέρουσες αποδείξεις τους και το σημαντικότερο: η κουλτούρα της ίδιας της
απόδειξης. Εδώ είμαστε θεατές άλλης μίας ασυνέπειας των συντακτών. Έπρεπε να
ξεκαθαρίσουν τις επιλογές τους:
Επιλογή 1. Δεν είναι σημαντικό να διδάσκουμε στοιχειώδη Ανάλυση. Αν
υποθέσουμε ότι αυτή υιοθέτησαν τότε τι χρειάζεται η έννοια του ορίου και της
συνέχειας που υπάρχει στο πρόγραμμα; Μπορεί κάποιος να κάνει θαυμάσια Calculus
και χωρίς αυτά. Για παράδειγμα θα μπορούσαν να διδαχθούν με κάποιες προσαρμογές
τα 15 πρώτα κεφάλαια από το
Morris Kline, Calculus, An Intuitive abd Physical Approach, Willey, 1977
στο οποίο έχω αναφερθεί και σε άλλο μήνυμα ή το πιο απλό
Kenneth L. Whipkey, Mary Nell Whipkey, The Power of Calculus, Willey,
1986
(αναφέρω δύο πηγές που τις έχω εύκαιρες, υπάρχουν πολλές άλλες και πιο
σύγχρονες).
Επιλογή 2. Είναι σημαντικό να διδάσκουμε στοιχεώδη Ανάλυση Αν
υποθέσουμε ότι ακολούθησαν αυτή την επιλογή θα μπορούσαν να παραμερίσουν το
υβριδικό παρελθόν που επεβλήθη από βιβλία που κάποιοι ήσαν και συγγραφείς τους,
να ξεκαθαρίσουν το τοπίο βάζοντας όρια στην πιάτσα και να μας παραδώσουν κάποια
λογική διάρθρωση με αποδείξεις και χωρίς ακρότητες (σχετικά βλ. εδώ
και εδώ).
04) Ο
υπερτονισμός της Στατιστικής. Είμαι ο τελευταίος που θα ισχυριζόμουν ότι
πρέπει να φεύγουν τα παιδιά από το σχολείο χωρίς γνωριμία με την Στατιστική και
τις Πιθανότητες. Θα ήθελα επίσης να προειδοποιήσω όσους διαβάζουν αυτή την
παράγραφο ότι για αυτά τα δύο κομμάτια των Μαθηματικών οι γνώσεις μου είναι οι
συνήθεις και δεν έχω ασχοληθεί ιδιαίτερα. Η γνώμη μου είναι ότι οι Πιθανότητες
πρέπει να διδάσκονται στο γενικό πρόγραμμα μόνο με τον κλασικό ορισμό και η
Στατιστική πάλι στο γενικό πρόγραμμα ως το κομμάτι που αντιστοιχεί στην
περιγραφική Στατιστική. Οι 28 ώρες (αν μέτρησα σωστά) που διατίθενται
αντιστοιχούν περίπου σε ένα μάθημα που διδάσκεται 2 ώρες εβδομαδιαίως στο 1ο
τετράμηνο και 1 ώρα στο δεύτερο. Πρόκειτα για υπερβολή και σπατάλη χρόνου.
Ειδικά η Στατιστική περιέχει κομμάτια ρουτίνας και εργασίες που θα μπορούσαν να
ανατεθούν σε ένα λογιστικό φύλλο (άν όχι μήπως πρέπει να επανέλθουμε και στους
λογαριθμικούς πίνακες;). Έτσι οι ώρες της Στατιστικής θα μπορούσαν να μειωθούν
στο μισό και να ικανοποιηθούν άλλες ανάγκες.
Ο αριθμός των ωρών (50 ώρες) που διατίθενται στην κατεύθυνση είναι επίσης
υπερβολικός. Η γνώμη μου είναι ότι η διδασκαλία της διωνυμικής κατανομής και
της κατανομής Bernoulli θα μπορούσαν να παραλειφθούν και ο χρόνος που θα
προέκυπτε θα μπορούσε να διατεθεί καλλίτερα. Π.χ. στην επαναφορά αποδείξεων που
οι συντάκτες των προγραμμάτων απομάκρυναν.
05)
Η κακοποίηση των διδακτικών στόχων. Η συζήτηση για τους
διδακτικούς στόχους διαρκεί πάνω από μισό αιώνα. Στην δεκαετία του 80 αποτέλεσε
βασικό θέμα συζήτησης για τα Αναλυτικά Προγράμματα. Η ιδέα ήταν ότι οι γενικοί
στόχοι της εκπαίδευσης και οι υπονοούμενοι στόχοι της διδασκαλίας πρέπει να εξειδικευθούν
περαιτέρω σε μαθήσεις που να περιγράφονται με μία παρατηρησιακή γλώσσα (μεταξύ
άλλων βλ. εδώ και εδώ). Παρά τις έντονες αντιδράσεις
κάποιων που θεωρούσαν ότι η χρήση των διδακτικών στόχων σήμαιναν και υιοθέτηση
της ψυχολογίας της συμπεριφοράς στην δεκαετία του 90 άρχισαν οι στόχοι να
εμφανίζονται ως βασικό στοιχείο των Προγραμμάτων. Αργότερα θεωρήθηκε
αναπόσπαστο στοιχείο και η παράθεση επιθυμητών δραστηριοτήτων. Οι διαφορές δεν
είναι αυτονόητες και γιαυτό στο ντοκουμέντο του προγράμματος σπουδών γίνεται
μία σχετική αναφορά (σ. 1951). Η κατάρτιση ενός προγράμματος με στόχους είναι
δύσκολη δουλειά για πολλούς λόγους. Αφ΄ενός μεν οι διατύπωση στόχων δε μπορεί με
όρους παρατηρήσιμης συμπεριφοράς δε μπορεί να γίνει παρά για απλές μαθήσεις και
αφ΄ετέρου χρειάζονται πολλοί απλοί διδακτικοί στόχοι. Ωστόσο ανάμεσα στην
δυσκολία του εγχειρήματος και στην διατύπωση προσχηματικών στόχων η απόσταση
είναι μεγάλη.
Για παράδειγμα τι καταλαβαίνει κανείς από τον παρακάτω στόχο;
2.4.2. Διερευνούν τις βασικές ιδιότητες της απόλυτης τιμής και τις
ερμηνεύουν γεωμετρικά (όσες είναι δυνατόν).
Απο τον παρακάτω;
2.5.1. Αναγνωρίζουν τη ν-οστή ρίζα μη αρνητικού αριθμού ως τη μοναδική μη αρνητική λύση της
εξίσωσης 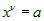 . .
Στο στόχο αυτό συγκαταλέγεται η εύρεση απλών ριζών όπως των 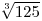 , ,
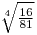 ;
Ας δούμε τον στόχο: ;
Ας δούμε τον στόχο:
6.1.1. Αναγνωρίζουν αν ένα πείραμα είναι πείραμα τύχης.
Εδώ πρόκειται για ένα στόχο που αναφέρεται σε μία έννοια για την οποία
ουσιαστικά δεν έχουμε ορισμό. Και επομένως δε μπορούμε παρά να περιμένουμε από
τους μαθητές να διακρίνουν χτυπητές περιπτώσεις πειραμάτων που δεν είναι
πειράματα τύχης.
Λ.χ. στην δραστηριότητα Δ32 της σελίδας 1970 το ε) είναι πείραμα τύχης; Αν όχι
πως θα εξηγήσουμε σε επόμενη τάξη ότι οι πολλαπλές μετρήσεις του ιδίου μεγέθους
ακολουθούν την κανονική κατανομή;
Έγραψα πιο πάνω ότι η παράθεση στόχων είναι προσχηματική. Να ένας λόγος. Στις
σελίδες 1979-1980 τα περιεχόμενα:
5.3. Εφαρμογές των παραλληλογράμμων (5 ώρες)
5.4. Χαρακτηριστικά σημεία τριγώνου: Έγκεντρο, Περίκεντρο, Ορθόκεντρο,
Βαρύκεντρο (5 ώρες)
5.5. Τραπέζια (2 ώρες)
έχουν για 12 ώρες μάθημα τους παρακάτω...τρείς (3) διδακτικούς στόχους:
5.3.1. Χρησιμοποιούν τις ιδιότητες των παραλληλογράμμων στην επίλυση
προβλημάτων.
5.4.1. Εντοπίζουν τις θέσεις του περικέντρου και του ορθοκέντρου ανάλογα με το
είδος του τριγώνου.
5.5.1. Αξιοποιούν την ιδιότητα της διαμέσου του τραπεζίου στην επίλυση
προβλημάτων.
06) ...κι
όλο στα ρηχά ψαρεύει. Κοιτώντας και ξανακοιτώντας τις 200 και πλέον
σελίδες του προγράμματος εντυπωσιάστηκα από ένα πράγμα: Την πλήρη απουσία
προσπάθειας των συντακτών του να προσδώσουν στις σπουδές κάποιο βάθος, κάποιο
είδος πληρότητας έστω και με θυσία της ευρύτητας. Να δουν τα παιδιά κάτι να
αρχίζει και να τελειώνει. Η υπεροχή των Μαθηματικών συνίσταται, μεταξύ άλλων,
στο να διατυπώνουν με συνοχή θεωρίες. Φέρνοντας μας σε ανάλογα διανοητικά
καθήκοντα: Να ερμηνεύουμε τον κόσμο και να εντάσσουμε τις ερμηνείες μας σε
συνεκτικές θεωρίες. Αν μάλιστα θέλήσουμε να τον αλλάξουμε προς το καλλίτερο
όπως προέτρεψε κάποιος σπουδαίος άνδρας ακόμη πιο καλά! Αντίθετα από αυτό
βλέπει κανείς διεσπαρμένα, θρυμματισμένα μικρά αποτελέσματα διανθισμένα με τις
περίφημες δραστηριότητες εν είδει χάπενινγκ. Απουσιάζουν οι αποδείξεις που
εννοιολογικά συνέχουν τα διάφορα κομμάτια, απουσιάζουν τα καθήκοντα που έθεσαν
στον εαυτό τους οι διάφοροι κλάδοι (μιγαδικοί για να επιλύουμε πολυωνυμικές
εξισώσεις, τριγωνομετρία για την επίλυση τριγώνων-τετραπλεύρων, όρια για να
βάλουμε σε στέρεη βάση την παράγωγο και το ολοκλήρωμα που μας ενδιαφέρει,
ακολουθίες για να καταλάβουμε καλλίτερα μέσω του διακριτού τα όρια, συνδυαστική
και επαγωγή για να μετρήσουμε/αποδείξουμε πλήθη/περιπτώσεις που δε μπορούμε να
διεκπεραιώσουμε στη μικρή ζωή μας. Αυτές οι διασυνδέσεις χάνονται. Γιατί;
Πιστεύω ότι αυτό γίνεται από συνειδητή επιλογή. Μία άλλη ομάδα συντακτών του
προγράμματος θα έκανε άλλες επιλογές. Και εξηγούμαι: Η πλειονότητα των ανθρώπων
που μετέχουν στην ομάδα των συνατκτών έχει ως κύρια ενασχόληση την Διδακτική
των Μαθηματικών. Ενδιαφέρονται κυρίως για την παρουσίαση των Μαθηματικών. Η
ενασχόληση που έχει αναπόφευκτα πολλή παρουσίαση και λίγα Μαθηματικά. Για να το
θέσω διαφορετικά: η διαδικασία κυριαρχεί της ουσίας. Πολλοί από αυτούς τους
ανθρώπους έχουν αφιερώσει πολύ χρόνο και σπουδές σε τέτοια ζητήματα. Μπορεί να
είναι βιρτουόζοι στο να κινούν πέρα δώθε χελώνες, να εντάσσουν έννοιες και
διαδικασίες σε τροχιές μάθησης, να παίζουν στα δάχτυλα τα επίπεδα Van Hiele, να
βλέπουν όλες τις δυνατές πολλαπλές αναπαραστάσεις μιας έννοιας, να βρίσκουν
"ενδύσεις" σε διάφορες μαθηματικές καταστάσεις και να δημιουργούν
"ρεαλιστικά προβλήματα", να χρησιμοποιούν τις ΤΠΕ στην εξερεύνηση
πρωτοβαθμίων-δευτεροβαθμίων-εκθετικών και άλλων καμπυλών, να μοντελοποιούν και
να προκαλούν εικασίες, να γνωρίζουν τα επιστημολογικά εμπόδια που αντιμετωπίζουν
οι μαθητές κ.α, κ.α. Ωστόσο δεν είναι τα Μαθηματικά η πρώτη προτεραιότητα τους.
Δεν θέλω να γενικεύσω: Ανάμεσα στην ομάδα των Συντακτών υπάρχουν άνθρωποι
μαθηματικά μορφωμένοι και ενήμεροι. Αλλά στην ζήση μας ο καθένας διαλέγει. Και,
πράγμα φυσιολογικό, μπορεί να δώσει περισσότερη σημασία σε κάτι παραμελώντας
κάτι άλλο. Και υπερασπίζοντας το λιγότερο. Αυτό που με θλίβει περισσότερο
απ΄όλα είναι ότι οι συντάκτες του προγράμματος, στην πλειονότητα τους, δεν
έννοιωσαν την ανάγκη να υπερασπιστούν τα Μαθηματικά. Το ότι στην ομάδα μετείχαν
αρκετοί σχολικοί σύμβουλοι μάλλον αύξησε την εντροπία.
07) Ακροτελεύτιο.
Η επιτροπή σύνταξης των προγραμμάτων είχε πολύ λίγο χρόνο να αντιμετωπίσει ένα
μεγάλο εγχείρημα. Λάθη και παραλείψεις είναι λογικό να υπάρχουν και για αυτές
υπάρχουν δικαιολογίες. Ωστόσο η δουλειά αποπνέει ένα είδος προχειρότητας. Και
δεν εννοώ (ή δεν εννοώ μόνο) το ότι ένα επίσημο ντοκουμέντο δημοσιευμένο σε ΦΕΚ
έχει φράσεις σε πρώτο ενικό ή εκφράσεις όπως "Γράφει το εξής αμίμητο"
(σ. 1943 υποσημ. 15) ή "κάτι τέτοια ξεσπάσματα τους προκαλούν
θυμηδία, αλλά μια και ο Descartes είναι αυτός που είναι, θυμάμαι κάτι που λέγαν
στο χωριό μου ότι τα πολύ ψηλά βουνά έχουν και...βαθιές χαράδρες"
(σ. 1943 υποσ. 13). Εννοώ ότι δεν φαίνεται οι συντάκτες του να έχουν σκεφτεί
αρκετά το θέμα της έκθεσης της ύλης, τις συνδέσεις, την οικονομία, την
πληρότητα (και άλλα σημαντικά που είμαι βέβαιος ότι θα επισημάνουν άλλοι
συνάδελφοι που θα συμμετάσχουν στην κουβέντα). Όλα αυτά μας εκθέτουν ως
μαθηματική συντεχνία (αν υποθέσουμε ότι είμαστε διατεθειμένοι να ασκούμε όλοι
το ίδιο επάγγελμα).
Το συγκεκριμένο πρόγραμμα παρεδόθη ως πεπραγμένο εν τέλει της προηγούμενης
κυβέρνησης και η εφαρμογή του ή μη εναποτίθεται στη νύν κυβέρνηση. Δεν ξέρω τι
κριτήρια θα πρυτανεύσουν. Αυτό που ξέρω είναι ότι οι εκπαιδευτικές ιδέες που
στήριξαν το υπό εξέταση πρόγραμμα διατρέχουν όλο το πολιτικό φάσμα. Και αυτό με
ανησυχεί.
|
|
![]()
![]()